红黑树

本文介绍红黑树的相关知识。本文主要参考开课吧胡船长的课程。本文的代码见red_black_tree.py

定义

红黑树是一种二叉搜索树。

首先，我们定义一下树的节点。如下代码，每个节点包含左孩子（left）和右孩子（right），val表示该节点的值。

class TreeNode:
    def __init__(self, val, color, left, right):
        self.val = val
        self.color = color
        self.left = left
        self.right = right

二叉搜索树

二叉搜索树是指，左子树中的节点均小于该节点，右子树中的节点均大于该节点。简单地说，就是

$\text{左子树} \lt \text{该节点} \lt \text{右子树}$

这条性质使得检索从 $O(n)$ 降到 $O(\log n)$，类似二分查找，每次可以排除一半的候选。

检索代码如下：

def search(self, val):
    def _search(node):
        if node is self.NIL:
            return self.NIL
        if val == node.val:
            return node
        elif val < node.val:
            return _search(node.left)
        else:
            return _search(node.right)
    return _search(self.root)

知道了二叉搜索树的主要性质，我们就遇到如下问题。

给定一些元素，如何构造二叉搜索树？

有很多关于二叉搜索树的构造方法。红黑树就是其中一种。所以红黑树算法，主要是为了解决二叉搜索树的构造问题。

红黑树的5条性质

红黑树在二叉搜索树的基础上，为每个节点定义了颜色信息。这些颜色信息仅供红黑树算法使用。

下面是红黑树算法的五条性质。

1. 每个节点非黑即红
2. 根节点是黑色
3. 叶子节点是黑色
4. 如果一个节点是红色，则其子节点是黑色
5. 从根节点出发到所有叶子节点的路径上，黑色节点数量相同

每个节点非黑即红

看似废话，实则有用。因为红黑树除了红色和黑色，还有第三种颜色，双重黑色。双重黑色节点会在删除节点后出现，随后算法会消除双重黑色。这个性质是说调整好的树没有节点是双重黑色。

def check1(self, node):
    if node is None:
        return True
    flag = node.color == self.RED or node.color == self.BLACK
    return flag and self.check1(node.left) and self.check1(node.right)

根节点是黑色

这条性质最容易检查和满足。每次调整完树，将根节点染成黑色即可。

def check2(self, node):
    return self.tree.root.color == self.BLACK

叶子节点是黑色

这里的叶子节点为NIL节点，即没有值的None节点。对于树中某个节点，若其没有左孩子，则表示其左孩子为NIL节点。一般的，NIL节点没有值，其颜色为黑色。

另一点需要说明的是，整棵树只有一个NIL节点实例，各个叶子节点均指向这个实例，即共享颜色。若NIL节点为红色，则所有叶子节点为红色。

def check3(self, node):
    if node is self.NIL:
        return node.color == self.BLACK
    assert node is not None
    return self.check3(node.left) and self.check3(node.right)

如果一个节点是红色，则其子节点是黑色

这条性质保证了没有双红的情况，即父节点为红色，子节点不能是红色。

def check4(self, node):
    if node is self.NIL:
        return True
    flag = True
    if node.color == self.RED:
        flag = node.left.color == self.BLACK and node.right.color == self.BLACK
    return flag and self.check4(node.left) and self.check4(node.right)

从根节点出发到所有叶子节点的路径上，黑色节点数量相同

某种程度上说，黑色节点控制了红黑树的平衡。注意由于根节点和叶子节点均为黑色，则一棵存在元素的树，路径黑色节点数量至少是2。

def check5(self, node):
    def black_count(node):
        if node is self.NIL:
            return 1
        left_count = black_count(node.left)
        right_count = black_count(node.right)
        if left_count != right_count or left_count == -1 or right_count == -1:
            return -1
        else:
            return left_count + node.color
    return black_count(self.tree.root) != -1

小结

根据以上的5条性质，我们可以得到一个结论。

红黑树中，从根节点到叶子节点的最长路径，至多是最短路径的 $2$ 倍。

红黑树的添加调整

如何在二叉搜索树中添加元素

算法很简单，先在该树中尝试查找该元素。由于不在树中，一定找不到。但在寻找的过程中，会找到一个叶子节点，意思是这个元素应该在这里，但目前这里没有元素。那我们就把这个新元素插入到这里。

def _add(node):
    if node is self.NIL:
        node = TreeNode(val, self.RED, self.NIL, self.NIL)
    elif val < node.val:
        node.left = _add(node.left)
    else:
        node.right = _add(node.right)
    return self._adjust_add(node)

然而这种策略会造成二叉树的不平衡，所以我们在插入后，需要调整一下树的平衡。

插入红色节点

首先，我们需要确定插入的节点是红色还是黑色。会发现，当插入

• 黑色：一定会调整。插入那条路径会多一个黑色节点。
• 红色：可能会调整。新节点的父节点是黑色时，不用调整；是红色时，需要调整。

综合来看，我们设定每次插入红色节点即可。

这里有一个问题：插入红色节点，需要调整时，为什么不将此节点设为黑色，反正要调整，没准黑色更好调整？

原因是这样写起代码来比较复杂，需要更多地分类讨论。且也没有看到有明显的改进。

故我们插入节点时，新节点的默认颜色为红色。

从爷爷的位置看

当我们一直插入红色时，势必会出现冲突。因为红色节点不能直接相连（简称为双红，即父子节点均为红色）。

当出现冲突时，我们需要调整树中节点的颜色。注意我们在调整颜色时，是一个递归过程。即叶子节点先出现的冲突，然后我们逐层向上调整。

调整插入节点的一个核心思路是从爷爷的位置看，下面我们来分析具体怎么看。

爷爷要把黑色给父辈，父辈们同意了

双红出现后，最简单的解决方法是，父节点向上要一个黑色。（思考一下为什么爷爷节点一定是黑色）

但爷爷节点要给父节点黑色时，需要同时给两个孩子。也就是要求父节点的兄弟也是红色，这时才能将爷爷的黑色下移一层。（在调整过程中，让每条路径的黑色节点数量不变）

如下图。这种调整可能会将冲突上移。也就是爷爷节点出现双红的情况。

爷爷要把黑色给父辈，父辈们不同意

当父辈们出现黑色时，爷爷的黑色就不能传给父辈。这时父亲就需要抢占爷爷的黑色，具体的，通过旋转将父亲节点旋转到爷爷节点的位置。

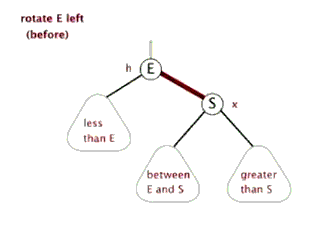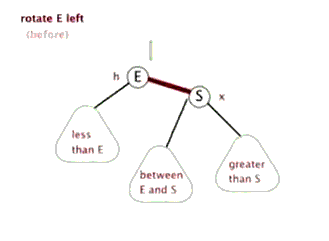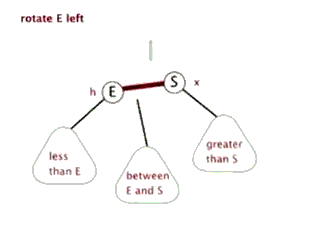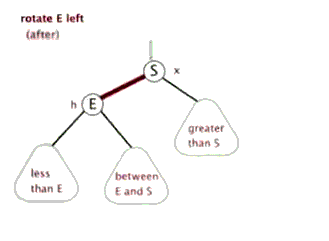
下面的动画展示左旋的过程：

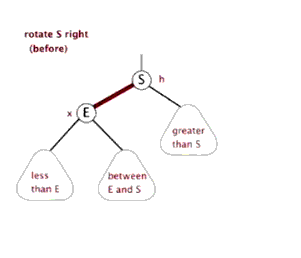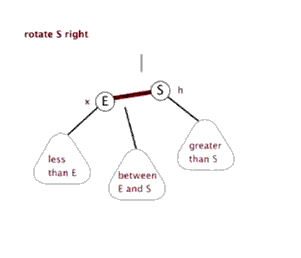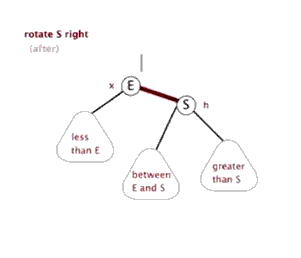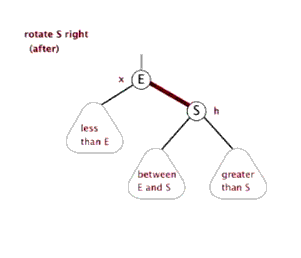
下面的动画展示右旋的过程：

当我们想让右边的孩子成为根节点，就是通过左旋，让右节点向左移动，成为中间的根节点。反之，右旋让左孩子向右移动，成为中间的根节点。

在红黑树中，父节点抢占爷爷节点会出现两种情况。

父节点可以直接抢占爷节点

如下图，父节点抢了爷爷的位置，并且抢了爷爷的黑色。爷爷只能接受父节点原来的红色。调整完之后，双红消失。

上述过程成功的关键在于，图中绿圈节点没有冲突。可以设想绿圈节点为红色，则这样调整过后，绿圈节点和父节点又形成双红。总结规律可以发现，无论左旋还是右旋，变更父节点的节点（即动图中的between E and S）不能是红色。这个节点在旋转前后，父节点发生变化，我们称此节点为变父节点。

父节点需要保证变父节点为黑色

当变父节点为红色时，我们只需要将其旋转为父节点即可。如下图。我们先将变父节点旋转为父节点，再让此父节点抢占爷节点。

红色上移

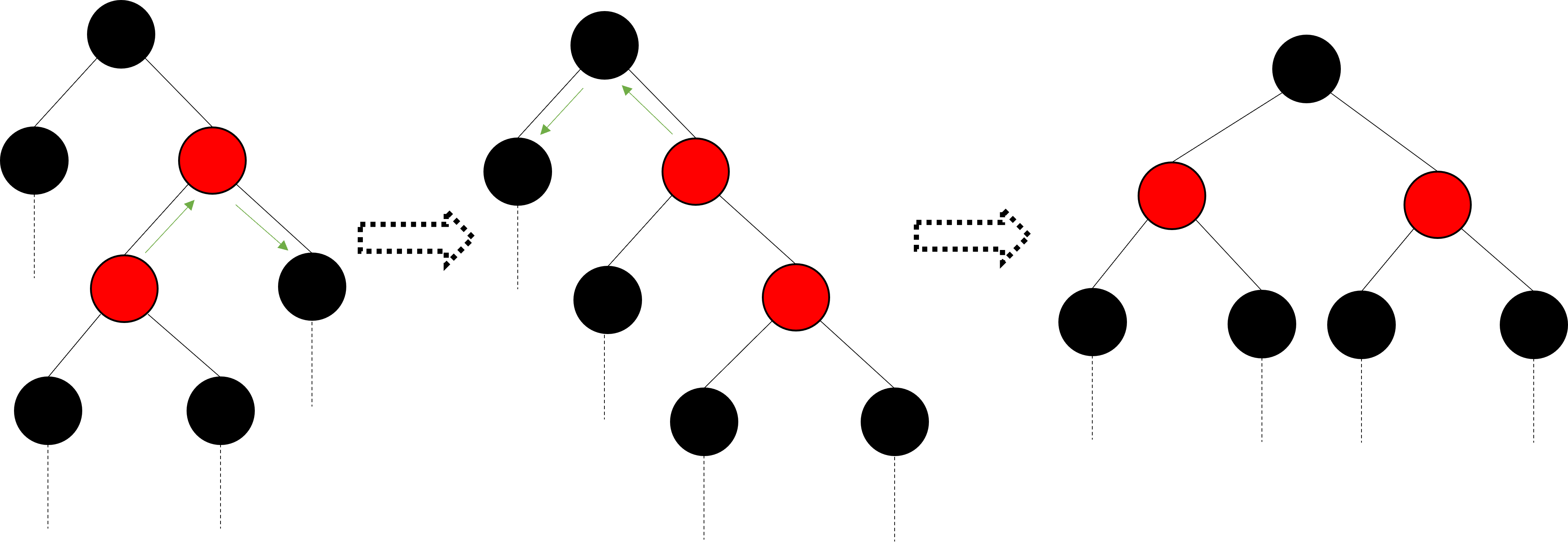
进行完旋转操作后，我们可以让红色上移。如下图，简单地染色即可实现。红色上移的目的是让树中的红色节点尽可能少。

代码

def add(self, val):
    def _add(node):
        if node is self.NIL:
            # 找到添加节点的位置，添加一个红色节点
            node = TreeNode(val, self.RED, self.NIL, self.NIL)
        elif val < node.val:
            node.left = _add(node.left)
        else:
            node.right = _add(node.right)
        # 调用_adjust_add调整，此时node为爷爷节点
        return self._adjust_add(node)

    self.root = _add(self.root)
    # 将根节点染成黑色
    self.root.color = self.BLACK

def _adjust_add(self, node):
    # 父节点都是黑色，必然没有双红，直接返回
    if node.left.color == self.BLACK and node.right.color == self.BLACK:
        return node
    recolor = False
    # 右父是黑色，不允许爷爷黑色下移
    if node.right.color == self.BLACK and node.left.color == self.RED:
        # 变父节点为红色，先将变父节点左旋为父节点
        if node.left.right.color == self.RED:
            node.left = self._rot_left(node.left)
        # 出现双红，父节点抢占爷节点
        if node.left.left.color == self.RED:
            node = self._rot_right(node)
            recolor = True
    # 左父是黑色，不允许爷爷黑色下移
    elif node.left.color == self.BLACK and node.right.color == self.RED:
        # 变父节点为红色，先将变父节点右旋为父节点
        if node.right.left.color == self.RED:
            node.right = self._rot_right(node.right)
        # 出现双红，父节点抢占爷节点
        if node.right.right.color == self.RED:
            node = self._rot_left(node)
            recolor = True
    # 爷爷可以直接黑色下移
    elif node.left.color == self.RED and node.right.color == self.RED:
        recolor = True
    # 红色上移
    if recolor:
        node.color = self.RED
        node.left.color = self.BLACK
        node.right.color = self.BLACK
    return node     

红黑树的删除调整

python中的红黑树实现-SortedList

相关阅读

• VScode配置Python开发环境
• 并查集